GNN

【GNN】- 1.初识GNN

Posted by Orchid on March 8, 2025

Introduction

什么是图神经网络（GNN）？简单来说，它是一种能够处理图结构数据的神经网络。类似之前所学习的，卷积神经网络（CNN）是处理图像数据（二维数据）的神经网络、循环神经网络（RNN）是处理序列数据的神经网络，图神经网络因为其所处理的数据类型而得以命名。

一句话简单概括一下图神经网络能够完成什么，实现怎样的效果：GNN 通过学习图中节点、边和全局特征的表示，能够有效地解决图相关的预测任务。

Graphs

首先，从抽象的角度来理解什么是图。学过数据结构的都知道，图这种数据结构，是由节点（node or vertex）和边（edge）组成的。在此基础上我们对图这一概念进一步的表示，图有以下三部分组成：

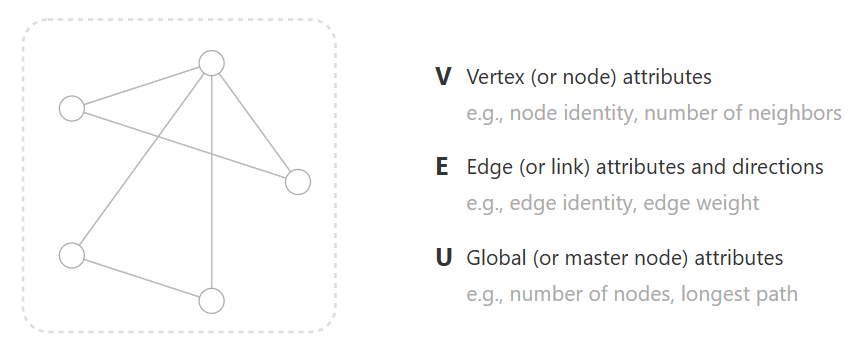
  1. 节点 Vertex
  2. 边 Edge
  3. 全局（整张图）Global

同时，每一部分都能够承载一定的信息，比如每一个节点可能包含其坐标信息、每条边可能包含其关联类别信息、整张图可能包含图的标签信息等等。也就是说图的每一个组成部分，除了作为构成图的一部分，还往往承载其相关的信息，这里将其定义为属性。而属性在计算机中往往表示为一个特征向量（embedding vector）：

Where to find graph

现在已经知道，图神经网络所处理的数据类型是图，但是哪里有图呢？总不可能真的拿一张“图”去给图神经网络学习吧。实际上图作为一种抽象的概念，蕴含在生活中的各处。一言以蔽之，只要能抽象出节点、边这样概念的数据，都可以称之为图。

比如图像数据，可以将每一个像素视作节点，像素与相邻的像素之间视为边，图像的标签可以视作图的标签：

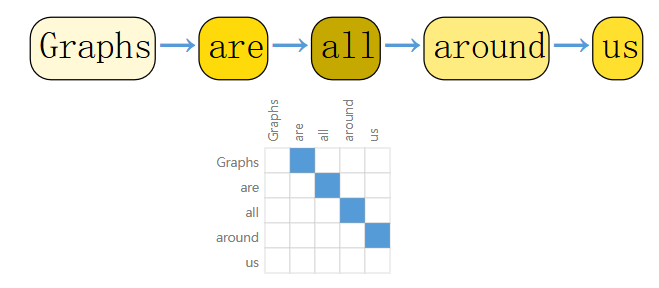
比如文本数据，可以将每一个词（token）视作节点，词与相邻的词之间视为边，整条文本的特殊含义视作图的全局信息：

比如分子结构，可以将分子中的每一个原子视作节点，原子与原子之间的键视为边，整个分子的类别视作图的全局信息：

当然，还有很多数据可以被抽象为图，比如社交网络、文献与文献间的引用网络等等。

What tasks it can do

我们已经知道了，图神经网络是基于图进行工作的，同时也学会了如何将生活中的数据抽象为图数据，接下来要看看图神经网络基于这些图数据具体能够实现什么样的预测任务：

  1. 图级任务（Graph-level tasks）：
    • 目标是预测整个图的属性，例如分子的性质或图的分类。
    • 输入：图
    • 输出：图的标签
  2. 节点级任务（Node-level tasks）：
    • 目标是预测图中每个节点的属性，例如节点分类或属性预测。
    • 输入：图
    • 输出：每个节点的标签
  3. 边级任务（Edge-level tasks）：
    • 目标是预测图中每条边的属性，例如边分类或链接预测。
    • 输入：图
    • 输出：每条边的标签

How to do: Message Passing

我们已经知道了图神经网络能够实现怎样的任务，那么它到底是基于怎样的原理来完成这些任务呢？同之前所有学习过的神经网络一样，我们可以将图神经网络视作一个函数，它以图信息为输入，以某种预期的值（图的标签、节点的标签、边的标签）为输出。所有的信息都已经蕴含在输入的图中了，图神经网络要干的事儿就是将这些信息整合、抽象、提取，再基于这些处理过后的信息去预测结果。在基于信息预测结果的部分，我们之前学过的 MLP 就可以胜任。因此，图神经网络干的关键事情，就是信息的整合、抽象、提取。

那么如何实现信息的整合、抽象、提取，这就不得不提GNNs 的核心机制是 消息传递（Message Passing），其是通过以下步骤实现：

  1. 消息构造（Message Construction）：

    • 每个节点从其邻居节点接收消息。消息可以是邻居节点的特征或边的特征。 \(m_{ij}^{(k)} = \Phi(h_i^{(k-1)},h_j^{(k-1)},e_{ij}^{(k-1)})\)

      • $m_{ij}^{(k)}$ 表示 $k$ 时刻从节点 $j$ 向节点 $i$ 传递的 message
      • $h_i^{(k-1)}$ 表示 $k-1$ 时刻从节点 $i$ 所包含的信息（embedding）
      • $e_{ij}^{(k-1)}$ 表示 $k-1$ 时刻边 $ij$ 所包含的信息（embedding）
      • $\Phi$ 是一个函数，可以是一个神经网络，用于抽象 $h_i^{(k-1)},h_j^{(k-1)},e_{ij}^{(k-1)}$ 三者包含的信息，以构造 $m_{ij}^{(k)}$

  2. 消息聚合（Message Aggregation）：

    • 节点将接收到的消息进行聚合，通常使用求和、求平均或取最大值等操作。 \(m_i^{(k)} = F_{j \in N(i)}(m_{ij}^{(k)})\)

      • $m_{i}^{(k)}$ 表示 $k$ 时刻从节点 $i$ 收到的总的 message
      • $F$ 往往选取一些具备 permutation invariant（排列不变性，输入顺序不影响输出结果）的方法，比如求和、求平均、求最大值

  3. 节点更新（Node Update）：

    • 节点根据聚合后的消息更新自身的特征。 \(h_i^{(k)} = σ(\phi(h_i^{(k-1)}, m_i^{(k)}))\)

      • $\phi$ 是一个函数，可以是一个神经网络，基于上一时刻节点 $i$ 的特征信息和这一时刻其收到的 message 更新其特征信息
      • $σ$ 是激活函数

通过上述消息传递（Message Passing）的流程，就实现了信息的整合、抽象、提取。

CATALOG